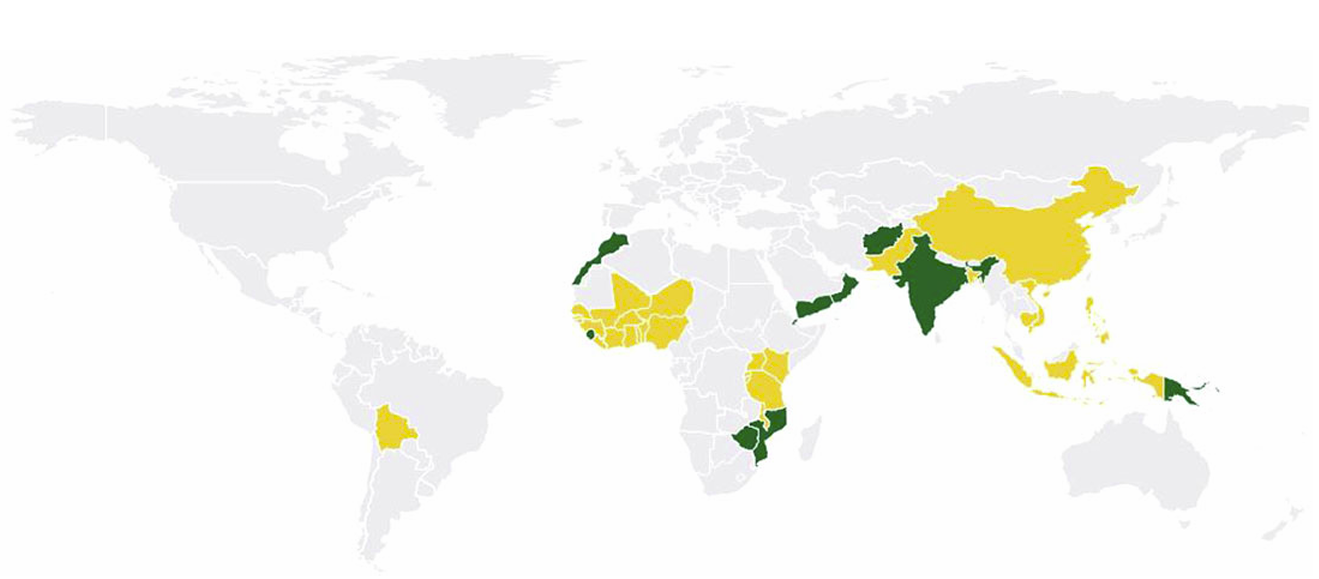
I referred to a 2018 paper on presence of vitamin A fortification in cooking oil of low-income countries to determine if there was any impact on life expectancy. Cooking oil provides a quite pervasive source of Vitamin A, because not only is it used to fry foods, it’s also often a key ingredient in baked goods. Many of the highlighted countries have been supplementing since the late 90’s and early 00’s, so there’s been over 20 years for some of the supposed benefits of vitamin A to show up in the data.
It states:
Figure 5.
Countries where edible oils are fortified with vitamin A (yellow) or vitamins A and D
(green).18 While 36 countries allow fortification of edible oils with vitamin A, 10 countries
(Afghanistan, Djibouti, India, Morocco, Mozambique, Oman, Papua New Guinea, Sierra
Leone, Yemen, and Zimbabwe) allow mandatory or voluntary fortification with vitamin A,
and mandate edible oils to include vitamin D as an optional or mandatory cofortificant in
their standards.
Focusing on female life expectancy because of greater stability, reducing outsized early deaths caused by accidents, war and violence.
Life expectancy data is from Factbook,
GDP per capita(PPP) is from Worldbank
Vitamin A Oil Fortified Countries vs Other Countries in Africa
This dataset includes both Yellow and Green coded countries and compares life expectancy to all other countries. This is a slightly more comprehensive list of Vitamin A supplemented countries. Factor_AD with a value of 1 means it’s a country includes vitamin A in the cooking oil, 0 means no Vitamin A in the oil. Each country is also weighted by country population.
import pandas as pd
import numpy as np # Ensure numpy is imported
# Define the data for Factor_AD
data = {
‘Country’: [
‘Ivory Coast’, ‘Malawi’, ‘Togo’, ‘Tanzania’, ‘Senegal’, ‘Kenya’, ‘Uganda’, ‘Ghana’,
‘Burundi’, ‘Rwanda’, ‘Guinea-Bissau’, ‘Guinea’, ‘Burkina Faso’, ‘Mali’, ‘Benin’, ‘Nigeria’,
‘Liberia’, ‘Niger’, ‘Seychelles’, ‘Libya’, ‘Tunisia’, ‘Algeria’, ‘Mauritius’, ‘Cabo Verde’,
‘Egypt’, ‘Morocco’, ‘Congo, Republic of the’, ‘South Africa’, ‘Gabon’, ‘Madagascar’,
‘Comoros’, ‘Eritrea’, ‘Sudan’, ‘Gambia, The’, ‘Ethiopia’, ‘Sao Tome and Principe’,
‘Zimbabwe’, ‘Zambia’, ‘Botswana’, ‘Djibouti’, ‘Mauritania’, ‘Namibia’, ‘Equatorial Guinea’,
‘Cameroon’, ‘Angola’, ‘Congo, Democratic Republic of the’, ‘Eswatini’, ‘Lesotho’,
‘South Sudan’, ‘Chad’, ‘Sierra Leone’, ‘Mozambique’, ‘Somalia’, ‘Central African Republic’
],
‘Life_Expectancy’: [
85.5, 76.1, 74.7, 72.6, 72.4, 72.2, 72, 71.8, 70.3, 68.6, 66.8, 66.6, 66.1, 65.6, 65, 64.2,
63.3, 62.5, 81.1, 80, 79.1, 78.7, 78.4, 76.7, 76.2, 76, 74.3, 73.5, 72.1, 70.3, 70.2, 70.2,
70.2, 70.1, 70, 69.4, 68.8, 68.7, 68.6, 68.5, 68.5, 67.6, 66.2, 66.1, 65.1, 64.6, 62.8,
62.3, 62.2, 62, 61, 59.6, 59, 57.7
],
‘Population_Percentage’: [
2.00, 1.40, 0.60, 4.60, 1.20, 3.80, 3.30, 2.30, 0.90, 1.00, 0.10, 1.00, 1.60, 1.60, 0.90, 15.30,
0.40, 1.90, 0.01, 0.50, 0.90, 3.10, 0.10, 0.04, 7.70, 2.60, 0.40, 4.10, 0.20, 2.10, 0.10, 0.30,
3.30, 0.20, 8.70, 0.02, 1.10, 1.40, 0.20, 0.10, 0.30, 0.20, 0.10, 2.00, 2.50, 7.00, 0.10, 0.20,
0.80, 1.30, 0.60, 2.30, 1.20, 0.40
],
‘FACTOR_AD’: [
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0
]
}
# Create DataFrame
df = pd.DataFrame(data)
# Convert percentage to weights
df[‘Weights’] = df[‘Population_Percentage’] / 100
# Group by FACTOR_AD and calculate weighted average life expectancy
result = df.groupby(‘FACTOR_AD’).apply(lambda x: np.average(x[‘Life_Expectancy’], weights=x[‘Weights’]))
print(result)
FACTOR_AD
0 70.176006
1 68.672134
dtype: float64
The correlation between the presence of FACTOR_AD and life expectancy is approximately -0.130. This indicates a weak negative correlation.
This is a far cry from what many would expect to see. The current dogma asserts it’s an essential nutrient.
Normalized for Confounding Variable
The most important confounding variable for life expectancy in this scenario would of course be wealth disparity between different countries. So, here’s the same calculation normalized for GDP per capita(PPP).
import pandas as pd
import numpy as np
# Define the data
data = {
‘Country’: [
‘Ivory Coast’, ‘Malawi’, ‘Togo’, ‘Tanzania’, ‘Senegal’, ‘Kenya’, ‘Uganda’, ‘Ghana’,
‘Burundi’, ‘Rwanda’, ‘Guinea-Bissau’, ‘Guinea’, ‘Burkina Faso’, ‘Mali’, ‘Benin’, ‘Nigeria’,
‘Liberia’, ‘Niger’, ‘Seychelles’, ‘Libya’, ‘Tunisia’, ‘Algeria’, ‘Mauritius’, ‘Cabo Verde’,
‘Egypt’, ‘Morocco’, ‘Congo, Republic of the’, ‘South Africa’, ‘Gabon’, ‘Madagascar’,
‘Comoros’, ‘Eritrea’, ‘Sudan’, ‘Gambia, The’, ‘Ethiopia’, ‘Sao Tome and Principe’,
‘Zimbabwe’, ‘Zambia’, ‘Botswana’, ‘Djibouti’, ‘Mauritania’, ‘Namibia’, ‘Equatorial Guinea’,
‘Cameroon’, ‘Angola’, ‘Congo, Democratic Republic of the’, ‘Eswatini’, ‘Lesotho’,
‘South Sudan’, ‘Chad’, ‘Sierra Leone’, ‘Mozambique’, ‘Somalia’, ‘Central African Republic’
],
‘Life_Expectancy’: [
85.5, 76.1, 74.7, 72.6, 72.4, 72.2, 72, 71.8, 70.3, 68.6, 66.8, 66.6, 66.1, 65.6, 65, 64.2,
63.3, 62.5, 81.1, 80, 79.1, 78.7, 78.4, 76.7, 76.2, 76, 74.3, 73.5, 72.1, 70.3, 70.2, 70.2,
70.2, 70.1, 70, 69.4, 68.8, 68.7, 68.6, 68.5, 68.5, 67.6, 66.2, 66.1, 65.1, 64.6, 62.8, 62.3,
62.2, 62, 61, 59.6, 59, 57.7
],
‘Population_Percentage’: [
2.00, 1.40, 0.60, 4.60, 1.20, 3.80, 3.30, 2.30, 0.90, 1.00, 0.10, 1.00, 1.60, 1.60, 0.90, 15.30,
0.40, 1.90, 0.01, 0.50, 0.90, 3.10, 0.10, 0.04, 7.70, 2.60, 0.40, 4.10, 0.20, 2.10, 0.10, 0.30,
3.30, 0.20, 8.70, 0.02, 1.10, 1.40, 0.20, 0.10, 0.30, 0.20, 0.10, 2.00, 2.50, 7.00, 0.10, 0.20,
0.80, 1.30, 0.60, 2.30, 1.20, 0.40
],
‘GDP_PPP_Per_Capita’: [
5939, 1658, 2380, 2932, 3768, 6178, 2397, 6500, 793, 2494, 2057, 2878, 2461, 2447, 3767, 5459,
1552, 1309, 29837, 23356, 11594, 13715, 22240, 7740, 13316, 10041, 3616, 14420, 15597, 1635,
3284, 1625, 4217, 2433, 2599, 4445, 2444, 3623, 19287, 5925, 5591, 9805, 18127, 4064, 7360,
1218, 9815, 2682, 1234, 1590, 1816, 1342, 1302, 1020
],
‘FACTOR_AD’: [
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0
]
}
# Create DataFrame
df = pd.DataFrame(data)
# Normalize GDP(PPP) per capita by the maximum value to scale between 0 and 1
df[‘Normalized_GDP’] = df[‘GDP_PPP_Per_Capita’] / df[‘GDP_PPP_Per_Capita’].max()
# Calculate the weighted life expectancy, where weights are the product of population percentage and normalized GDP
df[‘Weights’] = (df[‘Population_Percentage’] / 100) * df[‘Normalized_GDP’]
# Group by FACTOR_AD and calculate the weighted average life expectancy
result = df.groupby(‘FACTOR_AD’).apply(lambda x: np.average(x[‘Life_Expectancy’], weights=x[‘Weights’]))
print(result)
FACTOR_AD
0 73.665821
1 69.473564
dtype: float64
The correlation between the presence of FACTOR_AD_GDP_NORMALIZED and life expectancy is approximately -0.359. This indicates a moderate negative correlation.
Sadly, when accounting for GDP differences, the correlation gets even worse. This means that in two countries with equal amounts of wealth, the people without Vitamin A supplemented oil can expect to live 4.19 years longer. Or, the people with the Vitamin A supplemented oil can expect to live 4.19 years shorter. This matches the well documented vitamin A toxicity studies. It’s just nice to verify that for myself.
It has been demonstrated that vitamin A intake among well-nourished subjects may lead to decreased life quality and increased mortality rates (Bjelakovic et al. 2007, 2008, 2012, 2014
This result adds some credibility to the idea that “Vitamin” A deficiencies are being conflated with other nutrient deficiencies such as protein, zinc, B vitamins, iron, protein, magnesium, iodine, etc. Or it might be that the dosages being administered are too high.
Feel free to check my work or make suggestions.